5.1 Lineer Regression

Bir lineer regression modeli hedefi, nitelik girdilerinin ağırlıklandırılmış toplamı olarak tahmin etmeye çalışır. Öğrenilen ilişkinin lineer olması yorumlanabilirliği kolaylaştırır. Lineer regression modelleri uzun süre istatistikçiler, bilgisayar bilimcileri ve sayısal problemlerle uğraşan diğer insanlar tarafından kullanılmıştır.

Lineer modeller, sürekli bir hedef olan y'nin x niteliklerine olan bağlılığını modellemek için kullanılabilir. Öğrenilen ilişkiler lineerdir ve tekil bir örnek için şöyle gösterilir:

\[y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon\]

Bir veri tanesinin sonucu için yapılan tahmin, verinin sahip olduğu p tane niteliğin ağırlıklandırılmış toplamıdır. Beta'lar (\(\beta_{j}\)) öğrenilen ağırlıkları ya da katsayıları ifade eder. Toplamdaki ilk ağırlığa (\(\beta_0\)) intercept denir ve herhangi bir nitelikle çarpılmaz. Epsilon (\(\epsilon\)) parametreler öğrendiğimiz halde hala yaptığımız hata miktarı, yani tahmin ve asıl sonuç arasındaki farktır. Bu hataların Gaussian bir dağılımı takip ettiği varsayılır, yani hem negatif hem de pozitif yönde ve çok sayıda küçük - az sayıda büyük hata yaparız.

Optimal ağırlıkları hesaplamak için çeşitli metotlar kullanılabilir. En küçük kareler metodu genellikle hesaplanan ve asıl sonuçlar arasındaki farkların karelerinin toplamını minimize eden ağırlıkları bulmak için kullanılır:

\[\hat{\boldsymbol{\beta}}=\arg\!\min_{\beta_0,\ldots,\beta_p}\sum_{i=1}^n\left(y^{(i)}-\left(\beta_0+\sum_{j=1}^p\beta_jx^{(i)}_{j}\right)\right)^{2}\]

Optimal ağırlıkların nasıl elde edileceğinin detayına girmeyeceğiz, ama eğer ilginizi çektiyse “The Elements of Statistical Learning” (Friedman, Hastie and Tibshirani 2009)¹⁷ kitabındaki 3.2. bölümü ya da lineer regression modelleriyle ilgili diğer online kaynakları okuyabilirsiniz.

Lineer regression modellerinin en büyük avantajı lineerliktir: Tahmin etme sürecini basitleştirirler ve en önemlisi, bu lineer denklemlerin modüler seviyede yorumlanabilmesi (ağırlıkların yorumlanması) çok kolaydır. Lineer ve benzer modellerin, sosyoloji, psikoloji ve diğer sayısal araştırma alanlarında sıkça başvuruluyor olmasının temel sebebi budur. Örneğin, tıpta, hastanın klinik sonucunu tahmin etmek tek önemli şey değildir, aynı cinsiyet, yaş ve diğer niteliklerde ilacın etkisini yorumlanabilir bir şekilde hesaplamak da önemlidir.

Ağırlıklar tahmini güven aralıklarıyla beraber gelir. Güven aralıkları, ağırlık tahmini için "doğru" ağırlığı belli bir kararlılıkla içeren aralıktır. Örneğin, 2 ağırlığı için %95 güven aralığı 1'den 3'e olabilir. Bu aralığın yorumlanması şöyle olur: Bu tahmini yeni veriler için 100 kez tekrarlasaydık, güven aralığı 100 durumdan 95'inde doğru ağırlığı içerirdi (lineer regression'ın eldeki veri için doğru model olması durumunda).

Modelin "doğru" model olup olmadığı, verideki ilişkilerin yapılan varsayımlarla tutarlı olup olmadığına bağlıdır. Bu varsayımlar lineerlik, normallik, homoskedastisite (sabit varyans), bağımsızlık, niteliklerin sabitliği ve çoklu doğrusal bağlılığın yokluğu.

Lineerlik
Lineer regression modeli, tahmini niteliklerin bir lineer kombinasyonu olmaya zorlar; bu hem en güçlü hem de en zayıf yanıdır. Lineerlik yorumlanabilirliği sağlar. Lineer etkileri hesaplamak ve açıklamak kolaydır. Toplama içerdiklerinden faktörler kolayca ayırt edilebilir. Eğer niteliklerin birbiriyle ilişkili olduklarından veya bir niteliğin hedef değişkenle lineer olmayan bir ilişkisi olduğundan şüpheleniyorsanız, etkileşim terimleri ekleyebilir veya regression spline'lar kullanabilirsiniz.

Normallik
Eldeki niteliklere göre hedef değişkenin normal dağılımda olduğu varsayılır. Eğer bu varsayım ihlal edilirse, ağırlıklar için hesaplanan güven aralıkları geçersizdir.

Homoskedastisite (sabit varyans)
Hata terimlerinin varyansının tüm nitelik uzayı boyunca sabit olduğu varsayılır. Bir evin fiyatını evin büyüklüğünden (metrekare) tahmin etmeye çalıştığınızı düşünün. Evin büyüklüğünden bağımsız olarak tahmindeki hatanın sabit varyansa sahip olduğunu varsayan bir lineer model oluşturuyorsunuz. Bu varsayım pratikte genellikle geçersizdir. Ev örneğinde, tahmindeki hataların büyük evler için daha yüksek varyansa sahip olması mantıklıdır, çünkü fiyatlar daha yüksektir ve fiyattaki dalgalanmalar daha olasıdır. Lineer modelinizdeki ortalama hatanın (tahmin ve gerçek fiyat arasındaki ortalama fark) 50,000 Euro olduğunu düşünün. Eğer homoskedastisite varsayarsanız, ortalama hata olan 50,000 Euro'nun hem 1 milyonluk bir ev hem de 40,000 Euro'luk bir ev için aynı olduğunu varsaymış olursunuz. Bu mantıksızdır çünkü negatif fiyatların olabileceği anlamına gelir.

Bağımsızlık
Tüm veri örneklerinin diğerlerinden bağımsız olduğu varsayılır. Eğer tekrar tekrar ölçüm yaparsanız, bir hasta için birden çok kan testi yapmak gibi, veri taneleri (gözlemler) bağımsız değildir. Bağımsız olmayan veriler için karışık etki modelleri veya GEE'ler gibi özel bir lineer regression modeline ihtiyacınız olur. Eğer "normal" lineer regression kullanırsanız, modelden yanlış sonuçlar elde edebilirsiniz.

Niteliklerin sabitliği
Girdi nitelikler "sabit" kabul edilirler. Buradaki sabit, niteliklerin istatiktiksel değişkenler olarak değil, eldeki sabitler olarak kabul edildiği anlamına gelir. Bu, niteliklerin ölçümünde hata olmayacağı anlamına gelen gerçek dışı bir varsayımdır. Ancak, bu varsayımı yapmazsanız, girdilerdeki hata paylarını dikkate alan çok karmaşık hata modelleri kullanmanız gerekir; genelde bu istenmeyen bir durumdur.

Çoklu doğrusal bağlılığın yokluğu
Ağırlıkların hesaplanmasını karıştıracağından, aralarında güçlü korelasyonlar olan niteliklerle çalışmak istemezsiniz. İki niteliğin arasında güçlü korelasyonun olduğu bir durumda ağırlıkları hesaplamak sorunlu hale gelir çünkü niteliklerin etkileri toplamsaldır ve etkilerin hangi niteliğe atfedileceği belirsiz hale gelir.

5.1.1 Yorumlama

Bir lineer regression modelindeki ağırlığın yorumlanması, o ağırlığa karşılık gelen niteliğin türüne bağlıdır.

• Sayısal nitelik: Sayısal niteliğin bir birim artması tahmin edilen sonucu niteliğin ağırlığı kadar değiştirir. Sayısal niteliklere örnek olarak bir evin büyüklüğü düşünülebilir.
• İkili nitelik: Herhangi bir veri örneği için iki değerden birini alan niteliklerdir. "Evin bahçesi var" niteliği bu tür niteliklere örnek verilebilir. Değerlerden biri referans kategorisi olarak adlandırılır (bazı programlama dillerinde 0 ile kodlanır), "Bahçe yok" gibi. Niteliği referans kategorisinden diğerine değiştirmek hesaplanan sonucu niteliğin ağırlığı kadar değiştirir.
• Birden çok kategoriye sahip kategorik nitelik: Sınırlı sayıda değer alabilen niteliklerdir. "Halı, laminat, parke" kategorilerine sahio "zemin türü" niteliği örnek verilebilir. Çok kategorili bir nitelikle başa çıkmanın bir yolu, her kategorinin kendi ikili sütununa sahip olduğu one-hot kodlamadır. L tane kategoriye sahip bir kategorik nitelik için sadece L-1 tane sütuna ihtiyacınız vardır, çünkü L tane sütun kullandığınızda L. sütun gereksiz bilgi içerir (örneğin, bir veri örneği için 1'den L-1'e tüm sütunlar 0 değerine sahipse, bu niteliğin o veri örneği için değerinin L kategorisi olduğu anlaşılır). Her bir kategorinin yorumlanması, ikili niteliklerin yorumlanmasıyla aynıdır. R gibi bazı programlama dilleri, kategorik nitelikleri farklı şekillerde kodlamanıza olana sağlar; bunu bölümün ilerleyen kısımlarında inceleyeceğiz.
• Intercept \(\beta_0\): Intercept, tüm veriler için 1 değerini alan "sabit niteliğin" ağırlığıdır. Çoğu program intercept'i hesaplamak için bu "1" niteliğini otomatik olarak ekler. Yorumlanması ise şu şekildedir: Tüm sayısal nitelikleri sıfır ve kategorik nitelikleri referans kategorisi olan bir veri örneği için modelin yapacağı tahmin intercept ağırlığıdır. Intercept'in yorumlanması genellikle önemsizdir çünkü tüm değerleri sıfır olan bir gözlem anlamsızdır. Nitelikler standardize edildiğinde (ortalama 0, standart sapma 1) yorumlama anlamlı olur: O zaman intercept değeri, tüm değerleri niteliklerin ortalama değeri olan veri için yapılan tahmini temsil eder.

Bir lineer regression modelindeki nitelikler, aşağıdaki şablonlarla otomatik olarak yorumlanabilir.

Sayısal bir niteliğin yorumlanması

Diğer tüm niteliklerin değerleri sabit tutulduğunda, \(x_{k}\) niteliğindeki bir birimlik bir artış, y için yapılan tahmini \(\beta_k\) birim arttırır.

Kategorik bir niteliğin yorumlanması

Diğer tüm niteliklerin değerleri sabit tutulduğunda, \(x_{k}\) niteliğini referans kategorisinden diğer kategoriye değiştirmek, y için yapılan tahmini \(\beta_{k}\) birim arttırır.

Lineer modellerin yorumlanmasında bir diğer ölçü R-kare'dir. R-kare, hedef değişkenin toplam varyansının ne kadarının model tarafından açıklandığını ölçer. R-kare değeriniz ne kadar fazlaysa, modeliniz veriyi o kadar iyi açıklıyor demektir. Formülü şu şekildedir:

\[R^2=1-HKT/VKT\]

HKT, hata terimlerinin karelerinin toplamıdır:

\[HKT=\sum_{i=1}^n(y^{(i)}-\hat{y}^{(i)})^2\]

VKT, verideki varyansın kareleri toplamıdır:

\[VKT=\sum_{i=1}^n(y^{(i)}-\bar{y})^2\]

HKT, modeli oluşturduktan sonra geride kalan varyansı temsil eder; gerçek ve tahmini değerlerin farklarının kareleriyle hesaplanır. VKT, hedef değişkenin toplam varyansıdır. R-kare, elinizdeki varyansın ne kadarının oluşturduğunuz lineer model tarafından açıklanabileceğini söyler. R-kare genellikle 0 ve 1 arasında; veriyi hiç açıklamayan modeller için 0, verideki tüm varyansı açıklayabilen modeller için 1 olmak üzere değer alır. R-kare'nin herhangi bir matematiksel hata olmadan negatif bir değer alması da mümkündür; bu durum HKT VKT'den büyük olduğunda, yani model verideki trendi açıklamadığında ve hedefin ortalamasını tahmin olarak kullanmaktan daha kötü sonuç verdiğinde gözlemlenir.

Bu haliyle formülde bir sıkıntı vardır çünkü R-kare değeri, modeldeki nitelik sayısıyla beraber, bu nitelikler hedef hakkında hiçbir bilgi vermeyen nitelikler de olsa artar. Bu yüzden modelde kullanılan nitelik sayısını da hesaba katan, ayarlanmış R-kare değerini kullanmak daha uygundur: p niteliklerin sayısı ve n veri sayısı olmak üzere

\[\bar{R}^2=1-(1-R^2)\frac{n-1}{n-p-1}\]

Çok düşük (ayarlanmış) R-kare değerine sahip modelleri yorumlamak anlamsızdır, çünkü bu modeller varyansın büyük çoğunluğunu açıklamaz. Bu tür bir modelin ağırlıklarını yorumlamak anlamsız olacaktır.

Niteliklerin Önemi

Bir lineer regression modelindeki bir niteliğin önemi, niteliğin t-istatistiğinin mutlak değeriyle ölçülebilir. t-istatistiği, hesaplanan ağırlığın standart hatayla ölçeklendirilmiş halidir.

\[t_{\hat{\beta}_j}=\frac{\hat{\beta}_j}{SE(\hat{\beta}_j)}\]

Bu formülün bize ne söylediğini inceleyelim: Bir niteliğin önemi ağırlığı arttıkça artar; bu gayet mantıklı. Hesaplanan ağırlığın varyansı arttıkça (ki bu doğru değerden gittikçe daha az emin olduğumuz anlamına gelir) niteliğin önemi azalır; bu da gayet mantıklıdır.

5.1.2 Örnek

Bu örnekte hava durumu ve takvim bilgilerini kullanarak belli bir günde kiralanan bisiklet sayısını lineer regression modeliyle tahmin etmeye çalışacağız. Yorumlama için, hesaplanan regression ağırlıklarını kullanacağız. Nitelikler sayısal ve kategorik niteliklerden oluşuyor. Tabloda her bir nitelik için hesaplanan ağırlık, hesaplamanın standart hatası (SH) ve t-istatistiğinin mutlak değeri yer alıyor (|t|).

	Ağırlık	SH	|t|
(Intercept)	2399.4	238.3	10.1
seasonSPRING	899.3	122.3	7.4
seasonSUMMER	138.2	161.7	0.9
seasonFALL	425.6	110.8	3.8
holidayHOLIDAY	-686.1	203.3	3.4
workingdayWORKING DAY	124.9	73.3	1.7
weathersitMISTY	-379.4	87.6	4.3
weathersitRAIN/SNOW/STORM	-1901.5	223.6	8.5
temp	110.7	7.0	15.7
hum	-17.4	3.2	5.5
windspeed	-42.5	6.9	6.2
days_since_2011	4.9	0.2	28.5

Sayısal niteliğin yorumlanması (sıcaklık): Diğer tüm nitelikler sabit tutulduğunda, sıcaklıktaki 1 derece Celsius artış, tahmini kiralanan bisiklet sayısını 110.7 arttırır.

Kategorik niteliğin yorumlanması (hava durumu): Interpretation of a categorical feature (“weathersit”): Diğer niteliklerin değişmediği varsayıldığında, havanın yağışlı/fırtınalı/karlı olması tahmini kiralanan bisiklet sayısını -1905.5 düşürür. Hava sisli olduğunda kiralanan bisiklet sayısı hava iyi olduğunda kiralanan bisiklet sayısından -379.4 daha azdır.

Lineer regression modellerinin doğası gereği, yapılan her yorum "diğer tüm nitelikler sabitken" dipnotunu beraberinde getirir. Tahmini değer niteliklerin lineer kombinasyonudur. Elde edilen lineer denklem, nitelik/hedef uzayında bir hiperdüzlem belirtir (bir niteliğe sahip bir model için basit bir doğru gibi). Ağırlıklar, bu hiperdüzlemin belli yönlerdeki eğimleridir (gradyan). Bu tür modellerin iyi bir yanı, toplamsallıklarının her niteliğin yorumlanmasını diğerlerinden bağımsız kılmasıdır; denklemde niteliklerin etkileri (ağırlık çarpı niteliğin değeri) bir toplamla bir araya getirildiğinden bu böyledir. Bunun kötü yanı, yorumlamaların, niteliklerin ortak dağılımlarını görmezden gelmesidir. Bir niteliğin artıp diğerinin sabit kalması gerçekçi olmayan ya da çok düşük ihtimalle karşılaşabileceğimiz veri örneklerine denk gelir, örneğin evdeki oda sayısının artması evin büyüklüğü artmadan mümkün değildir.

5.1.3 Görsel Yorumlama

Lineer regression modellerini kolayca anlaşılabilir kılan birçok görselleştirme metodu vardır.

5.1.3.1 Ağırlık Grafiği

Ağırlık tablosundaki bilgiler (ağırlıklar ve varyans hesapları) bir ağırlık grafiğinde görselleştirilebilir. Aşağıdaki tablo yukarıda incelediğimiz lineer regression modelinin sonuçlarını gösterir.

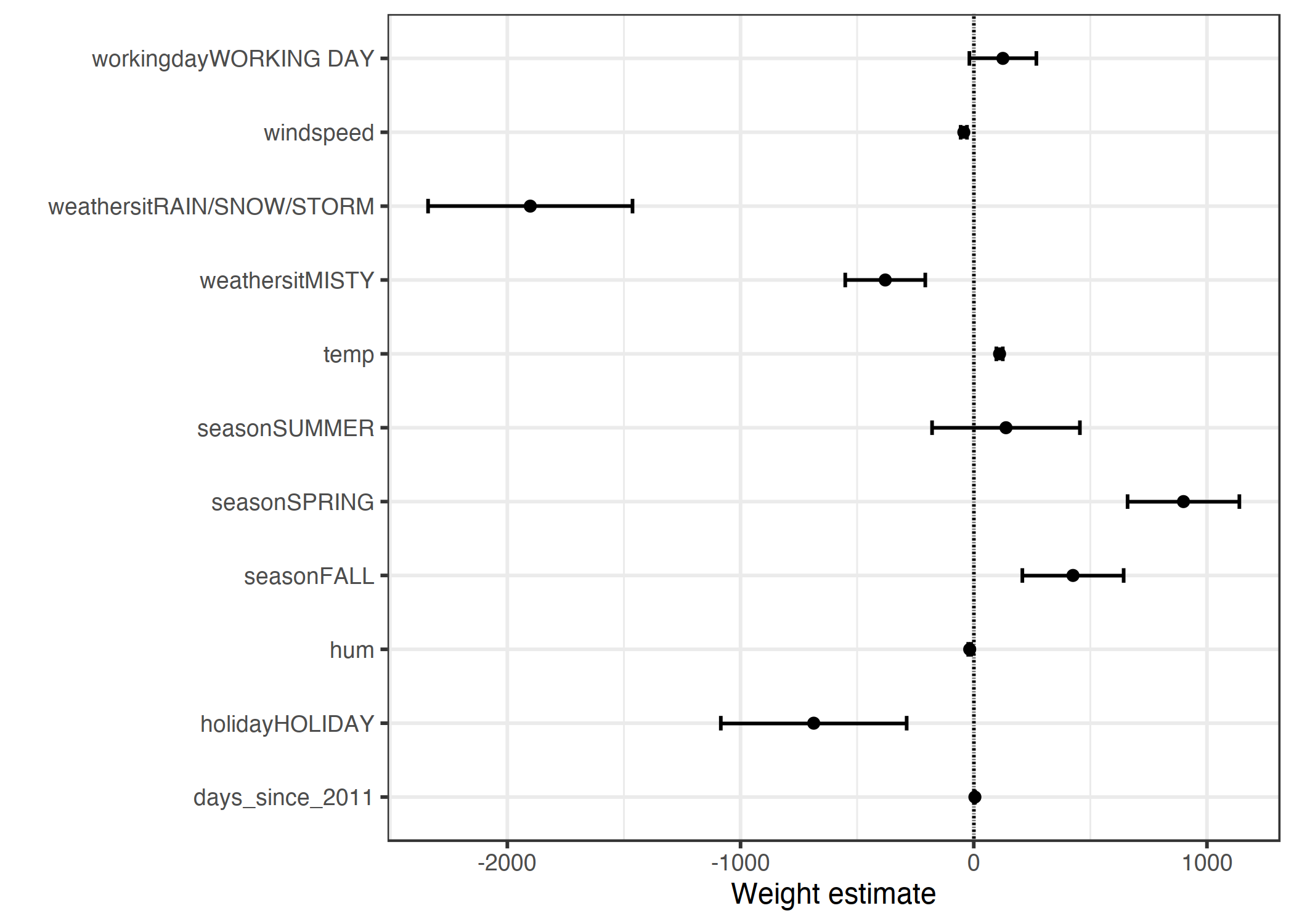
ŞEKİL 5.1: Noktalar ağırlıkları, çizgiler %95 güven aralıklarını temsil eder.

Grafik, yağışlı/karlı/fırtınalı havanın tahmini kiralanan bisiklet sayısına güçlü bir şekilde negatif yönde etki ettiğini gösteriyor. İş günü niteliğinin ağırlığının sıfıra çok yakın ve sıfırın güven aralığının içinde olması, niteliğin istatistiksel anlamda önemsiz olduğunu söylüyor. Sıcaklık gibi bazı nitelikler için güven aralığı çok kısa ve hesaplar sıfıra yakın, ama buna rağmen niteliğin istatistiksel anlamda etkisi önemli. Burada ağırlık grafiğiyle ilgili problem, niteliklerin farklı ölçü birimlerinde olması. Hava durumu nitelikleri için hesaplanan ağırlık iyi bir hava ile yağışlı/karlı/fırtınalı bir hava arasındaki farkı temsil ederken, sıcaklık niteliğinin ağırlığı 1 derece Celsius artışın etkisini temsil eder. Ağırlıkları karşılaştırılabilir kılmanın yolu, lineer modeli hesaplamadan önce nitelikleri ölçeklemektir (ortalamayı 0, standart sapmayı 1 yapacak şekilde).

5.1.3.2 Etki Grafiği

Ağırlıklar nitelik değerleriyle çarpıldığında daha anlamlı yorumlanabilirler. Ağırlıklar niteliklerin ölçeklerine bağlıdırlar, örneğin bir insanın boyunu ölçüyorsanız metre yerine santimetre kullanmanız bu niteliğe karşılık gelen ağırlığı değiştirir; ama etkisi aynıdır. Niteliğin verideki dağılımını da bilmeniz oldukça önemlidir, çünkü örneğin niteliğin düşük bir varyansa sahip olması, neredeyse her veri örneğinin bu nitelik için aynı etkiye sahip olduğu anlamına gelir. Etki grafiği, ağırlık ve nitelik kombinasyonunun yapılan tahmine ne kadar etki ettiğini anlamanızı sağlar. Etki grafiğini çizebilmek için etkileri hesaplamak gerekir: Etki, ağırlık çarpı niteliğin o veri tanesi için aldığı değerdir.

\[\text{etki}_{j}^{(i)}=w_{j}x_{j}^{(i)}\]

Daha sonra etkiler kutu grafikleriyle çizilebilir. Kutu grafiklerindeki kutular, elinizdeki verinin yarısı için etki aralığını içerir (%25'den %75'e etki çeyrekliği). Kutunun içindeki dik çizgi medyan etkisini, yani verilerin %50'sinin daha fazla etkiye sahip ve diğer %50'sinin daha az etkiye sahip olduğu değeri temsil eder. ÇAA çeyrekler arası aralık olmak üzere yatay çizgiler \(\pm1.5\text{ÇAA}/\sqrt{n}\) arasındadır (ÇAA, %75 çeyreklik ile %25 çeyreklik arasındaki farktır). Noktalar outlier değerleri temsil eder. Kategorik niteliklerin etkileri -her kategorinin kendisine özel satıra sahip olduğu ağırlık grafiğinin aksine- tek bir kutu grafiğinde özetlenebilir.

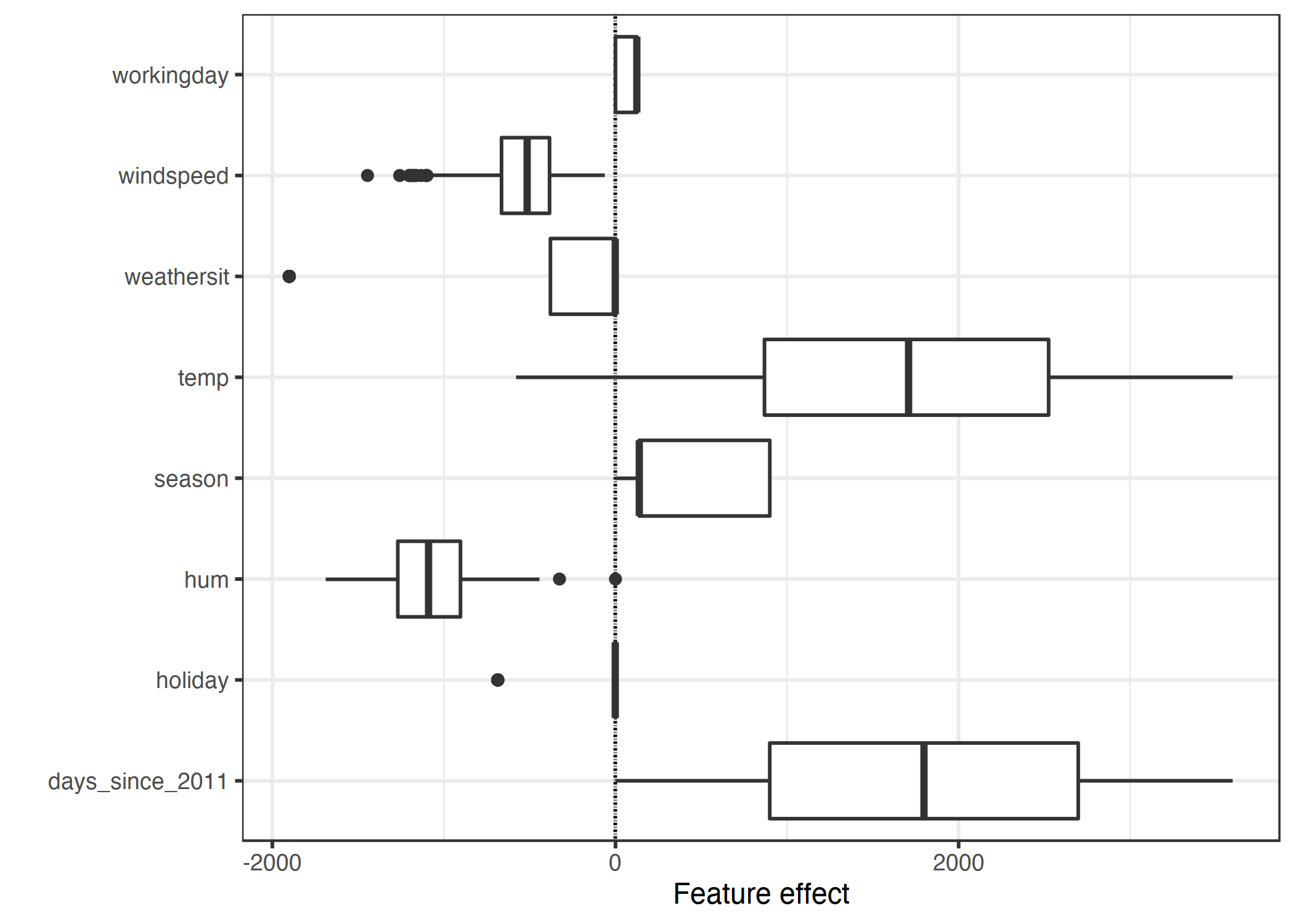
ŞEKİL 5.2: Etki grafiği, her nitelik için veri boyunca etkilerin (= niteliğin değeri çarpı ağırlığı) dağılımını gösterir.

Tahmin edilen kiralık bisiklet sayısına en büyük katkıyı sıcaklık ve hedef değişkenin trendini içeren geçen gün sayısı niteliği sağlıyor. Sıcaklık özelliğinin etkisi büyük bir aralık içinde değişiyor. Geçen gün sayısının etkisi sıfırdan büyük pozitif sayılara değişiyor; verideki ilk günün (01.01.2011) çok düşük bir trend etkisi var ve niteliğin ağırlığı pozitif (4.93). Bu, etkinin her geçen gün arttığını ve en yüksek değerini verideki son gün için aldığını gösteriyor (31.12.2012). Negatif etkiye sahip ağırlıklarda pozitif etkiye sahip veri örnekleri, negatif nitelik değerine sahip olan veriler olacaktır. Örneğin, rüzgar hızının yüksek negatif etkiye sahip olduğu günler (örnekler) rüzgar hızının yüksek olduğu günlerdir.

5.1.4 Tekil Tahminlerin Açıklanması

"Bir veri örneğinin nitelikleri, onun için yapılan tahmini ne kadar etkiledi?" sorusunu bu veri için etkileri hesaplayarak bulabiliriz. Tekil veri için etkilerin yorumlanması ancak diğer niteliklerin etkilerinin dağılımıyla karşılaştırıldığında anlamlıdır. Diyelim ki, lineer modelin verideki 6. örnek için yaptığı tahmini açıklamak istiyoruz. Verinin nitelik değerleri şu şekilde:

TABLE 5.1: Feature values for instance 6

Feature	Value
season	WINTER
yr	2011
mnth	JAN
holiday	NO HOLIDAY
weekday	THU
workingday	WORKING DAY
weathersit	GOOD
temp	1.604356
hum	51.8261
windspeed	6.000868
cnt	1606
days_since_2011	5

Niteliklerin etkilerini hesaplamak için nitelik değerleri ile modeldeki ağırlıkları çarpmalıyız. "workingday" (iş günü) niteliğinin "WORKING DAY" değeri için etki 124.9 olarak bulunur. 1.6 derece Celsius sıcaklık için etki 177.6 olarak hesaplanır. Bu tekil etkileri etkilerin tüm verideki dağılımlarını gösteren etki grafiğinde çarpıyla göstermek, tekil etkileri etkilerin dağılımıyla karşılaştırmamıza olanak sağlar.

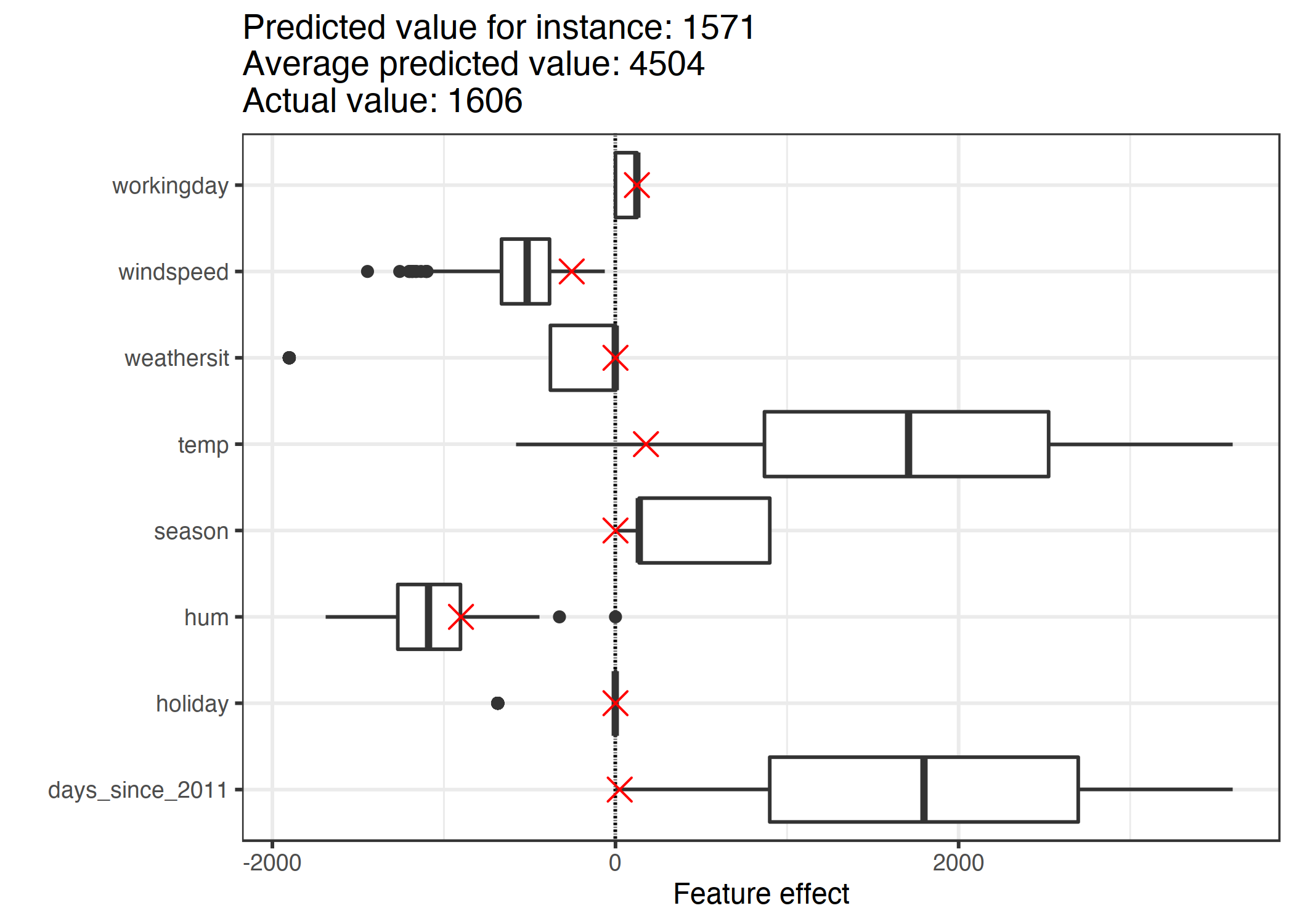
ŞEKİL 5.3: Tekil veri için etki grafiği, etki dağılımını verinin kendi etkileriyle beraber gösterir.

Tüm veri için yapılan tahminlerin ortalaması 4504 bisiklettir. Bu sayıyla karşılaştırıldığında 6. veri örneği için yapılan tahmin, 1571, küçük bir sayıdır; etki grafiği bunun nedenin bize gösterebilir. Grafikte gözlemlenebileceği üzere, 6. veri örneği düşük sıcaklık etkisine sahiptir çünkü o günün sıcaklık değeri 2 derece olup verideki çoğu günün sıcaklığından düşüktür (ve modelde sıcaklığın ağırlığı pozitiftir). Aynı zamanda, geçen gün sayısı niteliğinin etkisi diğer verilere göre daha düşüktür çünkü bu veri örneği 2011'in 5. gününe denk gelir, burada da bu niteliğin ağırlığı pozitiftir.

5.1.5 Kategorik Niteliklerin Şifrelenmesi

Kategorik nitelikleri şifrelemek için birkaç yöntem var ve ağırlıkların yorumlanması seçtiğiniz yönteme göre değişiklik gösterir.

Lineer regression modelleri için standart yöntem tedavi şifrelemesidir, ve çoğu durumda yeterli bir çözümdür. Farklı şifreleme yöntemleri, kategorik niteliğin sütunundaki değerleri tasarım matrisine yerleştirme şekillerinde ayrışır. Bu kısımda üç farklı şifreleme yöntemine bakacağız, ama tüm metotlar bunlarla sınırlı değil. İlk iki veri örneği için nitelik A kategorisi, üçüncü ve dördüncü için nitelik B kategorisi ve son ikisi için C kategorisi değerini alır.

Tedavi şifrelemesi

Tedavi şifrelemesinde ağırlıklar, referans kategorisi ve eldeki kategori arasında tahmin değerinde oluşan farktır. Modeldeki intercept terimi, diğer tüm nitelikler aynı kaldığında, referans kategorisinin ortalamasıdır. Tasarım matrisinin ilk sütunu intercept, yani tamamı 1'lerden oluşan bir sütundur. İkinci sütun verinin B kategorisinde olup olmadığını, üçüncü sütun ise C kategorisinde olup olmadığını belirtir. A kategorisi için bir sütuna ihtiyaç yoktur, çünkü bu durumda lineer denklem "overspecified" olur ve ağırlıklar için biricik çözüm bulunamaz. Verinin ne B ne de C kategorisinde olmadığını bilmek yeterlidir.

Nitelik matrisi: \[\begin{pmatrix}1&0&0\\1&0&0\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}\]

Etki şifrelemesi

Her kategori için ağırlık, diğer nitelikler sıfır veya referans değerini aldığında, o kategoriyle genel ortalama arasında tahmindeki farktır. İlk sütun intercept'i hesaplamak için kullanılır. Intercept'in ağırlığı olan \(\beta_{0}\) genel ortalamadır ve ikinci sütunun ağırlığı \(\beta_{1}\), genel ortalama ve B kategorisi arasındaki farktır. B kategorisinin toplam etkisi \(\beta_{0}+\beta_{1}\) olur. C kategorisinin yorumlanması da benzer şekilde yapılabilir. Referans kategorisi olan A için \(-(\beta_{1}+\beta_{2})\) genel ortalamayla aradaki fark ve \(\beta_{0}-(\beta_{1}+\beta_{2})\) genel etkidir.

Nitelik matrisi: \[\begin{pmatrix}1&-1&-1\\1&-1&-1\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}\]

Kukla şifrelemesi

Her kategori için \(\beta\), o kategori için hesaplanan ortalama y değeridir (diğer tüm niteliklerin değerlerinin sıfır veya referans değeri olduğu varsayımıyla). Burada lineer modelin ağırlıklarının biricik bir çözümünü bulabilmek adına intercept ihmal edilir. Bu çoklu doğrusal bağlılık problemi herhangi bir kategoriyi ihmal ederek de çözülebilir.

Nitelik matrisi: \[\begin{pmatrix}1&0&0\\1&0&0\\0&1&0\\0&1&0\\0&0&1\\0&0&1\\\end{pmatrix}\]

Kategorik niteliklerin farklı şifrelenme yöntemlerini incelemek istiyorsanız, bu sayfaya ve şu blog yazısına bakabilirsiniz.

5.1.6 Lineer Modeller İyi Açıklamalar Meydana Getirir Mi?

İnsan dostu açıklamalar kısmında bahsettiğimiz iyi bir açıklamanın gereklilikleri incelendiğinde, lineer modellerin en iyi açıklamalar için uygun olmadıkları görülür. Karşıtlıklardan faydalanırlar ama referans alınan veri örneği tüm sayısal değerlerin sıfır ve tüm kategorik değerlerin referans kategorisinde olduğu bir örnek olduğundan yapay ve anlamsızdır ve gerçekte verinizin içinde bulunma olasılığı çok düşüktür; bir istina dışında: Eğer tüm sayısal niteliklerde değerler ortalama merkezli hale getirilirse (niteliğin değeri eksi ortalama) ve tüm kategorik nitelikler etki şifrelemesiyle şifrelenirse, referans örneği tüm niteliklerin ortalama değerini aldığı örnek olur. Bu da var olmayan bir örnek olabilir, ama en azından karşılaşması daha olası ve daha anlamlıdır. Bu durumda hesaplanan nitelik etkileri, tahmine olan katkıyı bu "ortalam örneğe" bağıl olarak temsil eder. İyi bir açıklamanın diğer özelliği seçilebilirliktir ve lineer modellerde daha az nitelik kullanarak veya aralıklı lineer modeller kullanarak elde edilebilir. Ama normal halleriyle lineer modeller farklı açıklamalar için seçenekler sunan açıklamalar oluşturmaz. Lineer modeller, lineer denklem nitelikler ve hedef değişken arasındaki ilişki için uygun olduğu durumlarda gerçekçi açıklamalar oluştururlar. Lineer olmayan ilişkilerin ve birbiriyle etkileşimli niteliklerin sayısı arttıkça, lineer model daha kötü performans gösterecek ve açıklamalar daha az gerçekçi olacaktır. Lineerlik, açıklamaların daha genel ve basit olmasını sağlar, ki bence modellerin bu yapısı insanların açıklamalarda lineer modeller kullanmasının temel sebebidir.

5.1.7 Aralıklı Lineer Modeller

Şimdiye kadar seçtiğim örnekler gayet hoş duruyordu değil mi? Gerçekte, elinizdeki niteliklerin sayısı birkaç tane değil yüzlerce hatta binlerce olabilir. Peki o zaman lineer regression modelleri işe yarar mı? Yorumlanabilirlikleri hızla düşecektir. Niteliklerin örneklerden daha fazla olduğu durumlarla bile karşılaşabilirsiniz, o zaman standart bir lineer modeli hesaplayamazsınız bile. Bu durumlarda bizi kurtaracak olan şey modele aralıklılık (daha az nitelikle çalışabilmeyi) getirecek yöntemlerdir.

5.1.7.1 Lasso

Lasso, lineer modelleri aralıklı yapmak için otomatik ve elverişli bir yöntemdir. Açılımı "en küçük mutlak küçülme ve seçim operatörü"dür ve bir lineer regression modeline uygulandığında, nitelik seçimini ve ağırlıkların regularization'ını sağlar. Ağırlıkları optimize edeceğimiz şu minimizasyon problemini düşünelim:

\[min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_i^T\boldsymbol{\beta})^2\right)\]

Lasso bu optimizasyon problemine bir terim ekler:

\[min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_{i}^T\boldsymbol{\beta})^2+\lambda||\boldsymbol{\beta}||_1\right)\]

\(||\boldsymbol{\beta}||_1\) terimi, nitelik vektörünün L1-normu, büyük ağırlık değerlerinin seçilmesini önler. L1-normu kullanıldığından çoğu ağırlık sıfır değerini alır, diğerleriyse küçülür. Lambda parametresi (\(\lambda\)) regularization etkisinin gücünü kontrol eder ve genelde çapraz doğrulama ile ayarlanır. Özellikle lambda büyük olduğunda çoğu ağırlık sıfır değerini alır. Niteliklerin ağırlıkları lambda teriminin bir fonksiyonu olarak görselleştirilebilir. Her bir ağırlık aşağıdaki şekilde bir eğriyle gösterilmiştir:

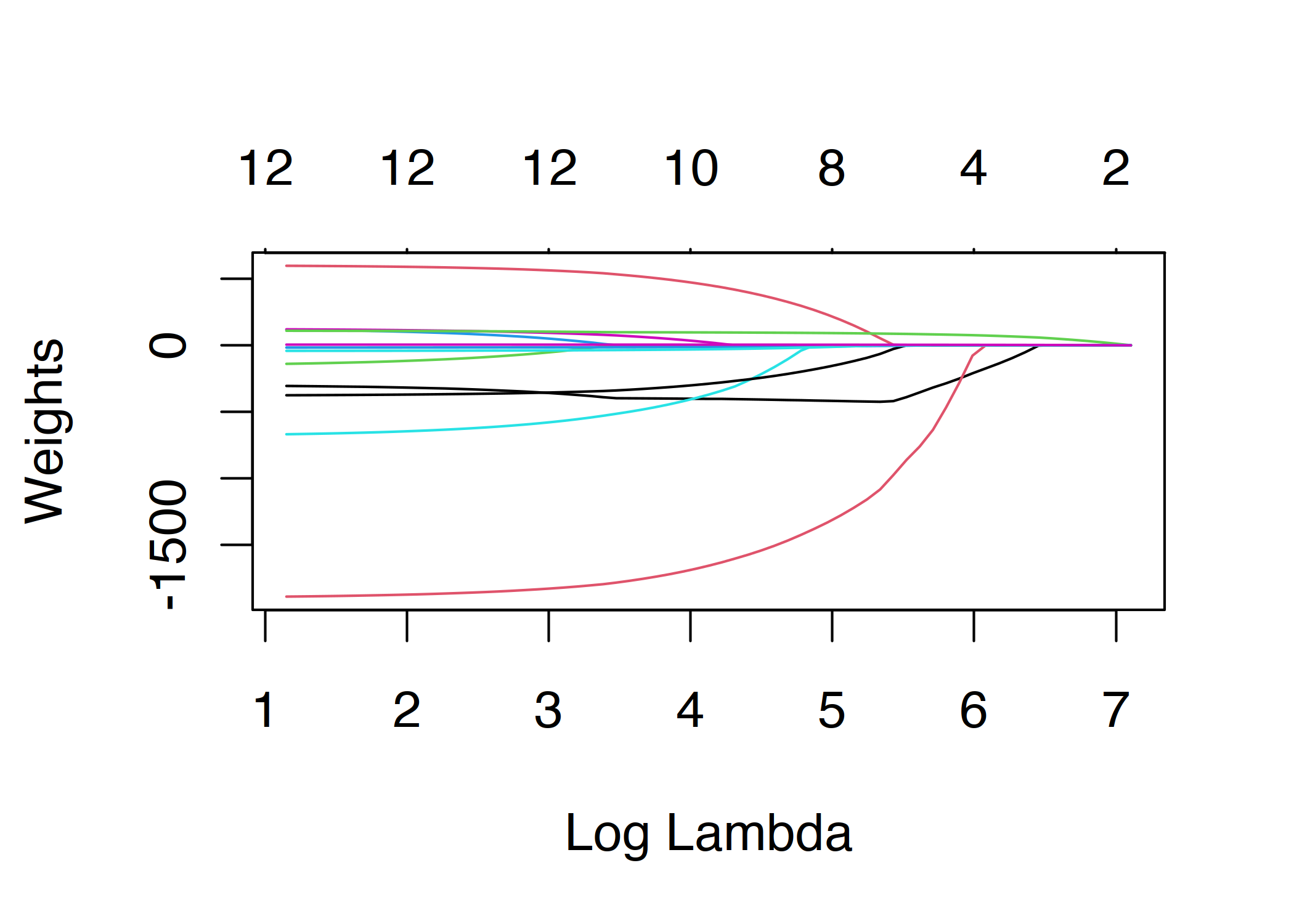
ŞEKİL 5.4: Lambda değeri arttıkça daha az nitelik sıfır olmayan bir ağırlık alır. Bu eğrilere regularization yolları da denir. Grafiğin üstündeki sayı sıfır olmayan ağırlık sayısıdır.

Peki lambda değerini nasıl seçmeliyiz? Terimi parametre kabul edip çapraz doğrulama yaparsak hatayı minimize eden lambda değerini bulabiliriz. Lambda, modelin yorumlanabilirliğini kontrol eden bir parametre olarak da düşünülebilir; değeri arttıkça model daha az nitelikle çalışır (çünkü bazı niteliklerin katsayıları sıfır olur) ve daha yorumlanabilir bir hale gelir.

Lasso'yla bir örnek

Lasso'yu kullanarak kiralanan bisiklet sayısını tahmin etmeye çalışacağız. Modelde kullanmak istediğimiz nitelik sayısını önceden 2 olarak belirleyelim.

	Weight
seasonWINTER	0.00
seasonSPRING	0.00
seasonSUMMER	0.00
seasonFALL	0.00
holidayHOLIDAY	0.00
workingdayWORKING DAY	0.00
weathersitMISTY	0.00
weathersitRAIN/SNOW/STORM	0.00
temp	52.33
hum	0.00
windspeed	0.00
days_since_2011	2.15

Lasso'nun sıfır olmayan bir ağırlık vermeyi seçtiği ilk iki nitelik sıcaklık ve geçen gün sayısı nitelikleri.

Şimdi de 5 nitelikle deneyelim:

	Weight
seasonWINTER	-389.99
seasonSPRING	0.00
seasonSUMMER	0.00
seasonFALL	0.00
holidayHOLIDAY	0.00
workingdayWORKING DAY	0.00
weathersitMISTY	0.00
weathersitRAIN/SNOW/STORM	-862.27
temp	85.58
hum	-3.04
windspeed	0.00
days_since_2011	3.82

Burada sıcaklık ve geçen gün sayısı niteliklerine verilen ağırlıkların farklı olduğuna dikkat edelim. Bunun sebebi lambdanın düşmesi "zaten" modelde olan nitelikleri daha az cezalandırır ve bu yüzden daha fazla mutlak değere sahip bir ağırlık verebilir. Lasso'nun verdiği ağırlıklar aynen normal lineer regression durumundaki ağırlıklar gibi yorumlanır. Sadece niteliklerin standardize edilip edilmediğini dikkat etmeniz gerekir, çünkü bu ağırlıkları etkiler. Bu örnekte nitelikler yazılım tarafından standardize edildi ama ağırlıklar orijinal ölçeklere uyacak şekilde geri dönüştürüldü. Note that the weights for “temp” and “days_since_2011” differ from the model with two features.

Lineer modelleri aralıklandırmak için diğer yöntemler:

Bir lineer modelin nitelik sayısını düşürmek için kullanabileceğiniz çokça metot vardır.

Önişleme metotları:

• Nitelikleri elle seçme: Nitelikleri seçmek için bir uzmana başvurabilirsiniz. Bu yöntemin kötü yanı otomatikleştirilememesi ve veriden anlayan birisine ihtiyacınızın olması.
• Tek değişkenli seçim: Bir örneği korelasyon katsayısıdır. Hedef değişkenle arasında belli bir değerin yukarısında korelasyon olan nitelikleri alırsınız. Dezavantajı nitelikleri tek başlarına değerlendiriyor olmasıdır; bazı nitelikler, lineer model onu diğerleriyle birlikte hesaba katmadan önce iyi bir korelasyon gösteremeyebilir. Bu tür nitelikleri tek değişkenli seçim metotlarını kullandığınızda gözden kaçırırsınız.

Adımlı metotlar:

• İleri yönlü seçim: Lineer modeli her nitelik için sadece o niteliği kullanarak hesaplayın ve en iyi çalışanı seçin (en yüksek R-kare değerine sahip olanı). Daha sonra bu modele diğer nitelikleri teker teker ekleyerek en iyi çalışanla sürece devam edin. Maksimum nitelik sayısı gibi bir kritere ulaştığınızda işlemi sonlandırın.
• Geri yönlü seçim: İleri yönlü seçime benzerdir, ama burada nitelik eklemek yerine tüm nitelikleri içeren modelle başlayıp en iyi performansa erişmek için hangisini çıkartmanız gerektiğini ararsınız. Yine bir kritere ulaşana kadar süreci devam ettirirsiniz.

Benim tavsiyem Lasso'dur, çünkü otomatiktir, tüm nitelikleri aynı anda değerlendirir ve lambda terimiyle kontrol edilebilir. Aynı zamanda logistic regression'la sınıflandırma için de çalışır.

5.1.8 Avantajlar

Tahminlerin ağırlıklandırılmış bir toplamla modellenmesi tahmin etme sürecini saydam kılar, ve Lasso ile kullanılan nitelik sayısının az olduğundan emin olabiliriz.

Lineer regression modellerinin kullanımı oldukça yaygın olduğundan birçok yerde tahmin amaçlı modelleme ve çıkarım için kullanılması uygun görülmüştür. Öğrenim materyalleri ve yazılım da dahil olmak üzere, üzerinde yüksek seviyede bir kolektif tecrübe ve uzmanlık vardır. R, Python, Java, Julia, Scala, Javascript gibi birçok programlama dilinde bulunabilir.

Matematiksel olarak bu ağırlıkları hesaplamak kolaydır ve optimal ağırlıkları bulacağınızın garantisi büyüktür (lineer regression varsayımlarının veriyle uyuşması halinde).

Ağırlıklarla birlikte güven aralıklarını, testleri ve sağlam istatistik teorisini elde edersiniz. Aynı zamanda lineer regression'ın birçok uzantısı vardır (GLM, GAM ve daha fazlası).

5.1.9 Dezavantajlar

Lineer regression modeleri yalnızca lineer ilişkileri, yani niteliklerin ağırlıklandırılmış toplamı olan hedefleri temsil edebilirler. Lineer olmayan veya niteliklerin birbiriyle etkileşimiyle ifade edilebilecek her değişkenin elle oluşturulması ve modele girdi olarka eklenmesi gerekir.

Aynı zamanda lineer modeller genelde iyi performans göstermezler, çünkü öğrenebilecekleri ilişkiler sınırlıdır ve gerçekliğin karmaşıklığını fazla basite indirgerler.

Ağırlıkların yorumlanması anlamsız gelebilir çünkü her biri diğer niteliklere bağlıdır. Hedef değişkenle yüksek korelasyona sahip iki nitelikten biri negatif ağırlık alabilir çünkü yüksek boyutlu uzayda diğer niteliğe göre korelasyonu negatiftir. Tümüyle korelasyona sahip nitelikler varken lineer denklem için biricik bir çözüm bulmak imkansızdır; örneğin elinizde ev fiyatı tahmin etmek için bir model olduğunu ve niteliklerinin oda sayısı ve ev büyüklüğü gibi şeyler olduğunu düşünün. Bu iki nitelik arasındaki korelasyon yüksektir; bir ev ne kadar büyükse, o kadar çok odası olur. Eğer her iki niteliği de modelde kullanmaya karar verirseniz, ev büyüklüğü niteliği ev fiyatının daha iyi bir belirleyicisi olabilir ve dolayısıyla daha yüksek bir ağırlık alabilir. Bu durumda oda sayısı niteliği negatif ağırlık alır, çünkü korelasyon çok yüksek olduğunda, büyüklüğü aynı bir evde oda sayısını arttırmak evin fiyatını düşürebilir veya lineer denklem daha kararsız hale gelebilir.

---

17. Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. “The elements of statistical learning”. www.web.stanford.edu/~hastie/ElemStatLearn/ (2009).↩︎