5.2 Logistic Regression
Logistic regression, iki farklı sonucu olan sınıflandırma problemlerinde olasılıkları modeller. Lineer regression modelinin sınıflandırma problemine uygun bir uzantısıdır.
5.2.1 Lineer regression modeli neden sınıflandırmada kullanılamaz?
Neden lineer regression modelleri regression problemlerinde iyi çalışır ama sınıflandırma yapamazlar? Olası iki sınıf olduğunda, birini 0 ve diğerini 1'le etiketleyip lineer regression kullanabilirsiniz; bu teknik olarak mümkündür ve model ağırlıkları bulabilir. Ama bu yaklaşımda birkaç sorun vardır:
Lineer modellerin çıktıları olasılıklar değildir, sınıflara sayılar gibi davranıp en iyi, yani veri noktaları ve hiperdüzlem (tek nitelikli bir modelde bir doğru) arasındaki mesafeleri minimize eden hiperdüzlemi bulmaya çalışır; noktalar arasında kalır ve yorumlayabileceğiniz olasılıklar elde edemezsiniz.
Aynı zamanda böyle bir durumda lineer modeller sıfırdan küçük veya birden büyük tahminler de yapacaktır. Bu noktada sınıflandırma için daha iyi bir yaklaşım olması gerektiğini görürüz.
Tahmin edilen sonuç bir olasılık değil noktalar arasında lineer bir fonksiyon olduğundan, bir sınıfı diğerinden ayırmak için kullanabileceğiniz anlamlı bir eşik değeri de yoktur. Bu durumu iyi anlatan bir görsel şu Stackoverflow sayfasında mevcut.
Lineer modeller birden çok sınıfa sahip sınıflandırma problemlerinde kullanılamaz. 2, 3 şeklinde etiketlemeye devam etmeniz gerekir. Sıralamanın bir anlamı olmasa da lineer model, nitelikler ve tahmini sınıflar arasına garip bir ilişki dayatmaya çalışır. Pozitif ağırlığa sahip bir niteliğin değeri arttıkça, büyük sayıyla etiketlenmiş sınıfın tahmin edilmesine katkı artar, birbirine yakın sayılarla etiketlenmiş sınıfların uzak sayılarla etiketlenenlerden daha yakın bir ilişkisi olmasa da.
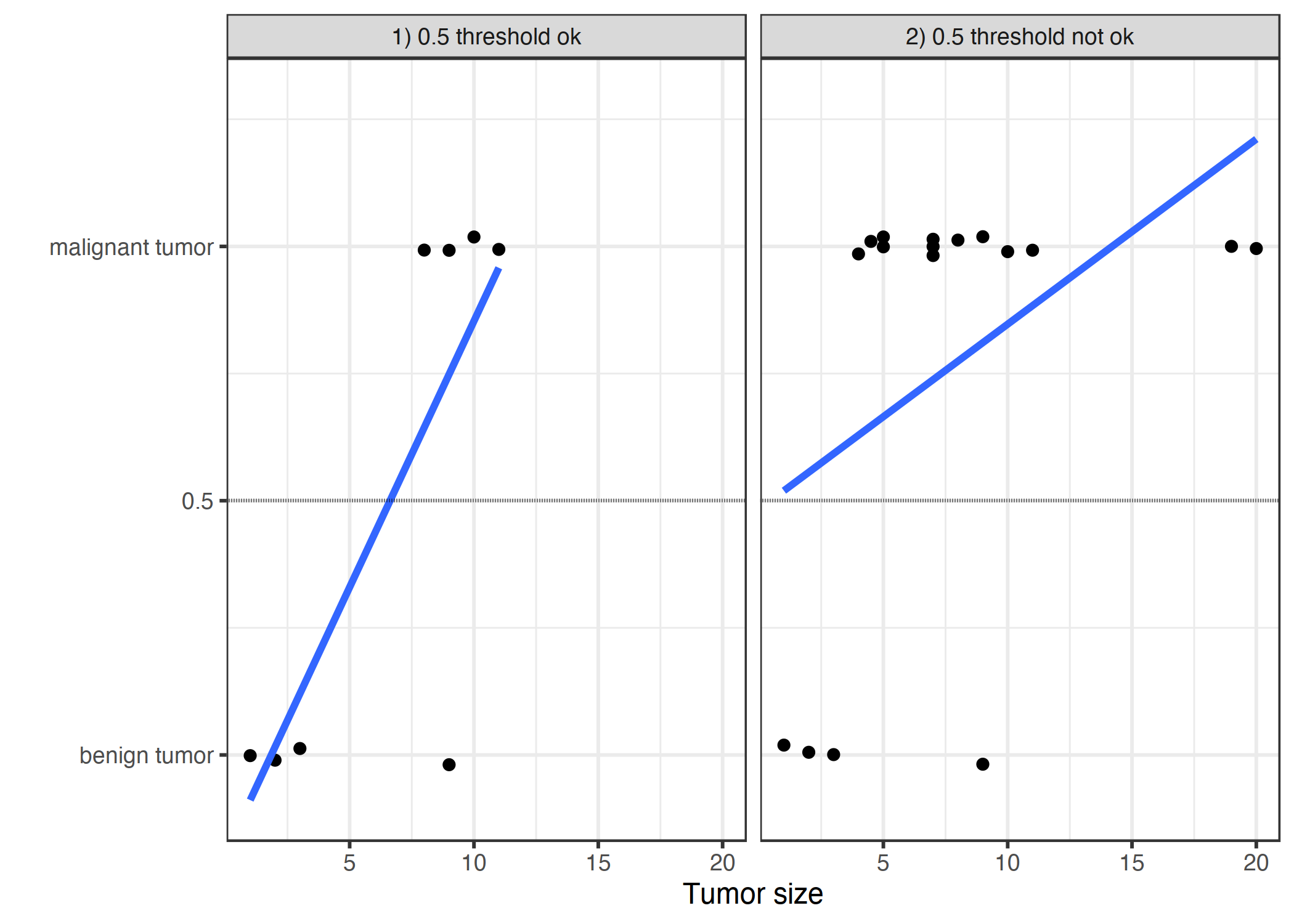
ŞEKİL 5.5: Bir lineer model tümörlerin büyüklüklernden iyi (0) veya kötü (1) huylu olup olmadığını tahmin etmeye çalışıyor. Çizgiler lineer modelleri gösteriyor. Soldaki veri için 0.5 bir eşik değeri olarak çalışabilir, fakat veriye birkaç kötü huylu tümör daha eklendiğinde regression çizgisi kayar ve 0.5 artık sınıfları ayırabilen bir eşik değeri değildir.
5.2.2 Teori
Logistic regression sınıflandırma problemlerine uygun bir metottur. Bir doğru veya hiperdüzlem kullanmak yerine, logistic regression modeli lineer denklemin sonucunu 0 ve 1 arasına sıkıştırmak için logistic fonksiyonunu kullanır:
\[\text{logistic}(\eta)=\frac{1}{1+exp(-\eta)}\]
Grafiği şu şekildedir:
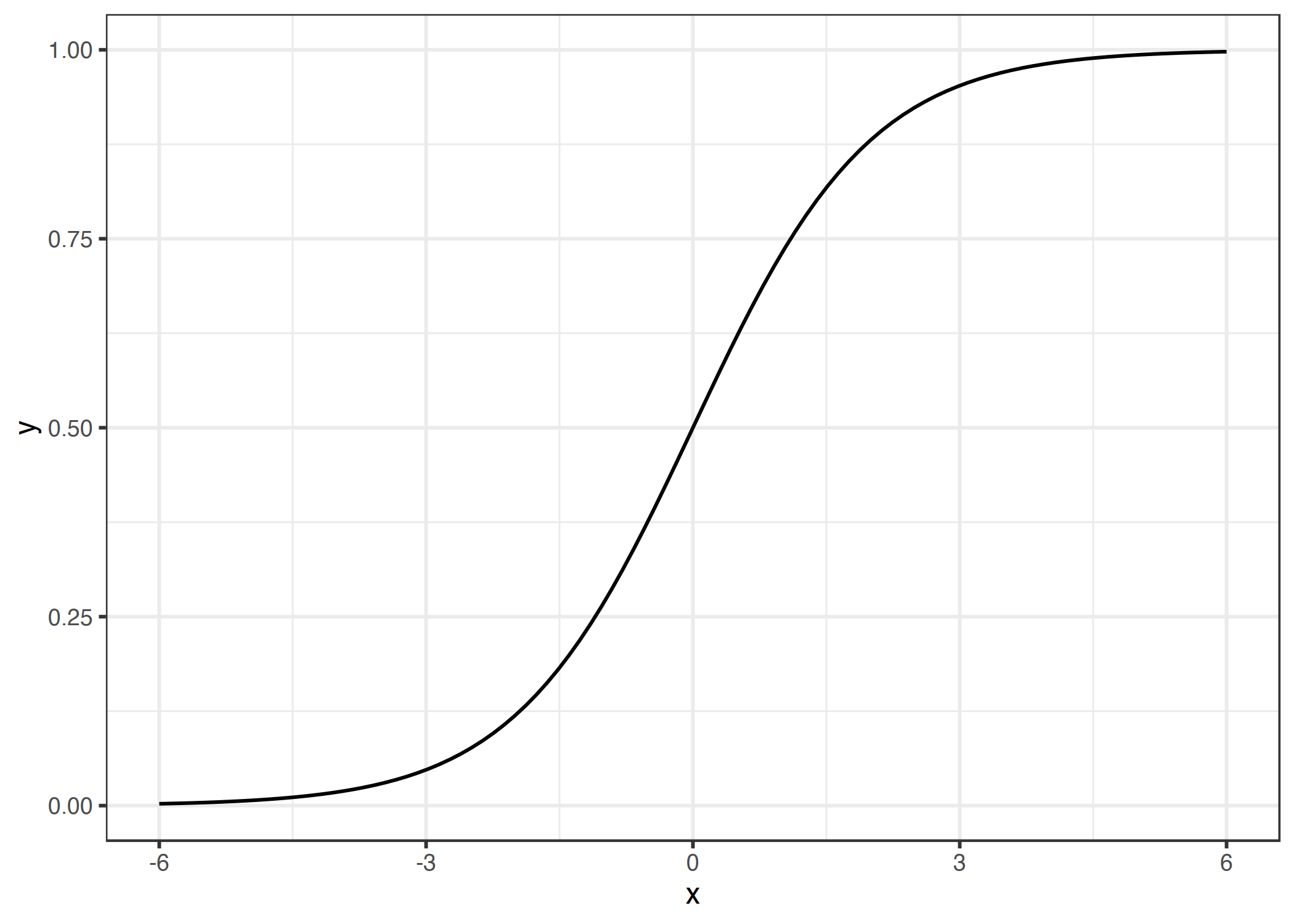
ŞEKİL 5.6: Logistic fonksiyonu, değer kümesi 0 ve 1 arasındadır. 0 girdisi için 0.5 verir.
Lineer regression'dan logistic regression'a geçiş çok kolaydır. Lineer regression modelinde, sonuç ve nitelikler arasındaki ilişkiyi bir lineer denklemle ifade ederiz:
\[\hat{y}^{(i)}=\beta_{0}+\beta_{1}x^{(i)}_{1}+\ldots+\beta_{p}x^{(i)}_{p}\]
Sınıflandırma için 0 ve 1 arasında değerleri tercih ettiğimizden, bu lineer denklemi logistic fonksiyonun içine yazarız. Çıktılar artık yalnızca 0 ve 1 arasındadır.
\[P(y^{(i)}=1)=\frac{1}{1+exp(-(\beta_{0}+\beta_{1}x^{(i)}_{1}+\ldots+\beta_{p}x^{(i)}_{p}))}\]
Tümör büyüklüğü örneğine logistic regression ile geri dönelim:
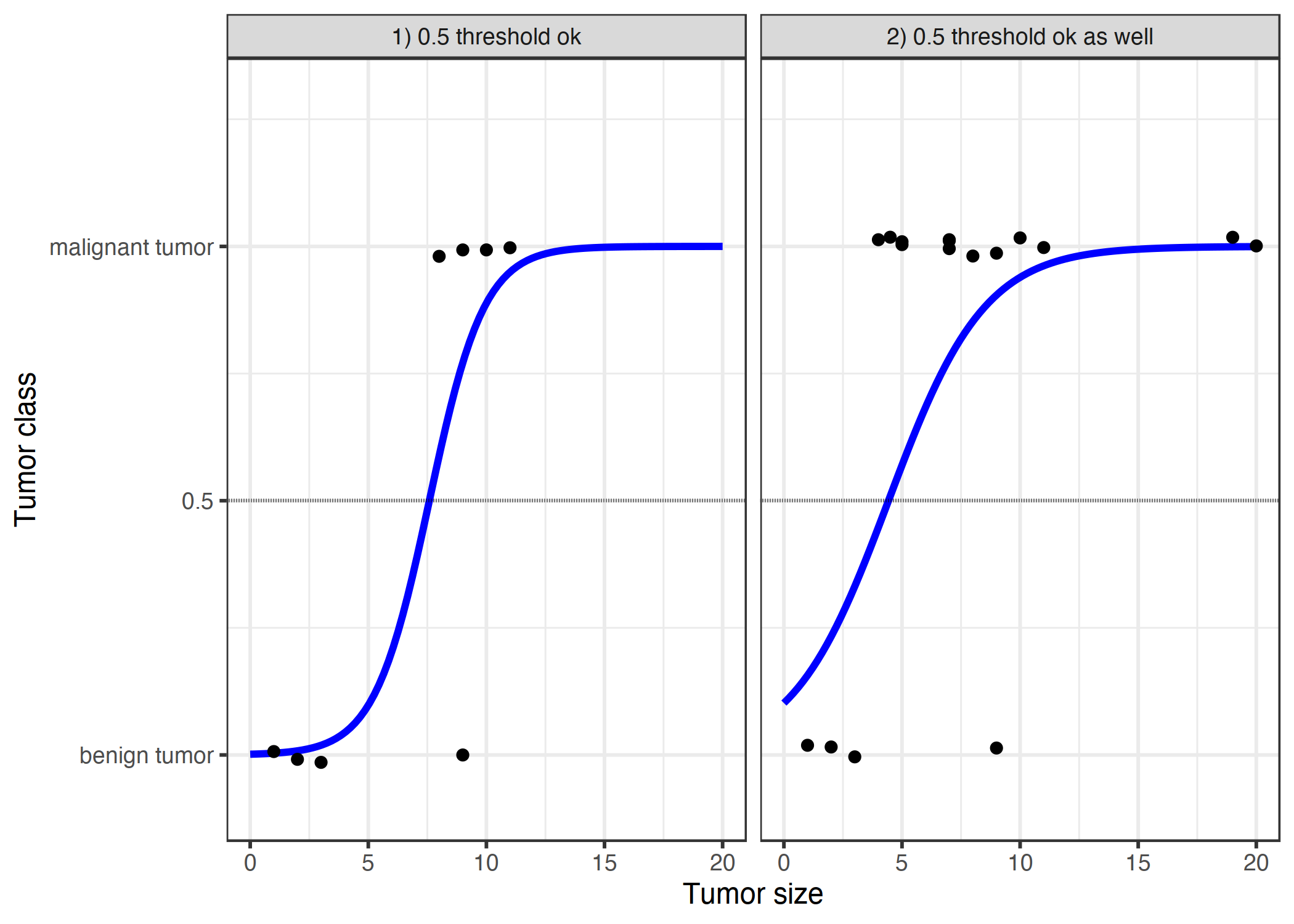
ŞEKİL 5.7: Logistic regression modeli, iyi ve kötü huylu tümörler arasındaki doğru karar sınırını bulur.
Logistic regression modeli sınıflandırma için daha uygundur ve 0.5 değeri her iki durumda da eşik değeri olarak çalışabilir. Eklenen veri noktaları hesaplanan eğriyi fazla etkilemez.
5.2.3 Yorumlama
Logistic regression modelinde çıktı 0 ve 1 arasında bir olasılık değeri olduğundan ağırlıkların yorumlanışı lineer regression modelinden farklıdır. Artık ağırlıklar olasılığı lineer olarak etkilemez. Ağırlıklandırılmış toplam logistic fonksiyonu ile bir olasılık değerine dönüştürülür. Yorumlayabilmek adına denklemi sadece lineer terim sağ tarafta kalacak şekilde tekrar yazmamız gerekir.
\[ln\left(\frac{P(y=1)}{1-P(y=1)}\right)=log\left(\frac{P(y=1)}{P(y=0)}\right)=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\]
ln() fonksiyonunun içindeki terime "odds" (bir olayın olma olasılığı bölü olmama olasılığı) denir ve logaritması alındığında log odds olur.
Bu formülde logistic regression modelinin log odds için bir lineer model olduğunu görüyoruz, ama bu hala işe yarar durmuyor. Terimleri biraz karıştırarak tahminin niteliklerden (\(x_j\)) biri 1 birim değiştiğinde nasıl değiştiğini görebilirsiniz. Bunun için denklemin her iki tarafını exp() fonksiyonuna alalım:
\[\frac{P(y=1)}{1-P(y=1)}=odds=exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\right)\]
Şimdi de niteliklerden biri 1 birim arttığında gerçekleşen değişime bakalım, ama fark yerine oranı hesaplayalım:
\[\frac{odds_{x_j+1}}{odds}=\frac{exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{j}(x_{j}+1)+\ldots+\beta_{p}x_{p}\right)}{exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{j}x_{j}+\ldots+\beta_{p}x_{p}\right)}\]
Aşağıdaki kuralı uygulayalım:
\[\frac{exp(a)}{exp(b)}=exp(a-b)\]
Ve terimleri çıkaralım:
\[\frac{odds_{x_j+1}}{odds}=exp\left(\beta_{j}(x_{j}+1)-\beta_{j}x_{j}\right)=exp\left(\beta_j\right)\]
Sonunda bir niteliğin ağırlığının exp() fonksiyonundaki değeri gibi sade bir değer elde ettik. Herhangi bir nitelikteki 1 birimlik değişim, odds oranını (çarpımsal) \(\exp(\beta_j)\) kat değiştirir. Bunu şu şekilde de yorumlayabiliriz: \(x_j\) niteliğindeki 1 birimlik bir değişim log odds değerini o niteliğe karşılık gelen ağırlık kadar arttırır. Odds oranına sıklıkla başvurulur çünkü bir değerin ln() fonksiyonundaki değerini düşünmek zihin için zordur, ama odds oranını yorumlamak kolaydır. Örneğin, odds değeri 2 ise, y=1'in olasılığı y=0'ın olasılığından iki kat daha fazladır. Eğer ağırlık (= log odds oranı) 0.7 ise, karşılık gelen niteliği 1 birim arttırmak odds değerini exp(0.7) ile (yaklaşık 2 ile) çarpar ve odds değeri 4 olur. Ama genelde odds değeriyle değil odds oranı olarak ağırlıklarla ilgilenirsiniz, çünkü odds değerini hesaplamak için her niteliğin değerini bilmeniz gerekir, ki bu da tekil bir veri noktasıyla ilgileniyorsanız anlamlıdır.
Farklı tipte niteliklere sahip logistic regression modelleri için yorumlama şu şekilde olur:
- Sayısal nitelik: Eğer \(x_{j}\) niteliğinin değerini 1 birim arttırırsanız, hesaplanan odds değeri \(\exp(\beta_{j})\) kat değişir.
- İkili kategorik nitelik: Niteliğin değerlerinden biri referans kategorisi (bazı dillerde 0 ile şifrelenen kategori) olarak adlandırılır. \(x_{j}\) niteliğini referans kategorisinden diğerine değiştirmek hesaplanan odds değerini \(\exp(\beta_{j})\) kat değiştirir.
- İki kategoriden daha fazla değere sahip kategorik nitelikler: Çok kategoriyle başa çıkmanın bir yolu one hot şifrelemedir, bu durumda her kategorinin kendi sütunu olur. L kategoriye sahip bir nitelik için sadece L-1 sütuna ihtiyacınız vardır, yoksa aşırı parametrize etmiş olursunuz. L. kategori referans kategorisi olarak adlandırılır. Lineer regression'da kullanılan herhangi bir şifreleme metodunu burada da kullanabilirsiniz. Şifreleme tamamlandığında her bir kategorinin yorumlanması ikili kategorik nitelikteki gibi olur.
- Intercept \(\beta_{0}\): Tüm sayısal niteliklerin değerleri sıfır ve tüm kategorik nitelikler referans kategorisinde olduğunda, odds değeri \(\exp(\beta_{0})\) olur. Intercept ağırlığının yorumlanması genelde önemsizdir.
5.2.4 Örnek
Bazı risk faktörlerine dayanarak rahim ağzı kanseri varlığını tahmin etmek için logistic regression kullanacağız. Aşağıdaki tabloda hesaplanan ağırlıklar, ilgili odds oranları ve tahminlerin standart hataları yer alıyor.
| Weight | Odds ratio | Std. Error | |
|---|---|---|---|
| Intercept | -2.91 | 0.05 | 0.32 |
| Hormonal contraceptives y/n | -0.12 | 0.89 | 0.30 |
| Smokes y/n | 0.26 | 1.30 | 0.37 |
| Num. of pregnancies | 0.04 | 1.04 | 0.10 |
| Num. of diagnosed STDs | 0.82 | 2.27 | 0.33 |
| Intrauterine device y/n | 0.62 | 1.86 | 0.40 |
Sayısal bir niteliğin yorumlanması ("Teşhis edilen STD sayısı"): Diğer tüm nitelikler sabitken, teşhis edilen STD (cinsel yolla bulaşan hastalıklar) sayısındaki artış kanser olasığı için odds değerini (kanser olma olasılığı bölü olmama olasılığı) 2.27 kat arttırır. Burada korelasyonun zorunlu olarak nedensellik belirtmediğini hatırlayalım.
Kategorik bir niteliğin yorumlanmnası (“Hormonal kontraseptifler (evet/hayır)”): Hormonal kontraseptif kullanan kadınlar için odds değeri kullanmayan kadınlara göre 0.89 kat daha azdır; diğer tüm niteliklerin sabit olduğunu varsayarsak.
Lineer modellerde olduğu gibi tüm yorumlar "diğer tüm nitelikler sabitken" varsayımını içerir.
5.2.5 Avantajlar ve dezavantajlar
Lineer regression modelinin avantaj ve dezavantajlarının çoğu logistic regression için de geçerlidir. Logistic regression geniş çapta çokça kullanılıyor olsa da, eldeki durumu açıklarken kısıtlı özgürlüğe sahiptir (etkileşim niteliklerini kendiniz eklemeniz gerekir) ve daha iyi performans gösteren modeller mümkündür.
Bir diğer dezavantaj ise, ağırlıkların yorumu çarpımsal ilişki barındırdığından yorumlamanın zor olmasıdır.
Logistic regression modelleri, mutlak ayrılmaya maruz kalabilir. Eğer elinizde hedef değişkeni çok iyi sınıflandırabilecek bir nitelik varsa logistic regression modeli hesaplanamaz, çünkü bu durumda o niteliğin ağırlığının sonsuz olması gerekir ve çözüme yaklaşılamaz. Böyle işe yarar bir niteliği kullanamamak kötüdür, ama zaten böyle bir durumda makine öğrenmesine ihtiyacınız kalmaz. Mutlak ayrılma ağırlıkların değer aralığına bir sınırlandırma getirerek (regularization) ya da ağırlıklar için önceden bir olasılık dağılımı tanımlayarak çözülebilir.
Logistic regression modellerinin iyi yanı modelin sınıflandırma yapmanın yanında size olasılık değerleri vermesidir. Bu sadece sınıflandırma kararını çıktı veren modellere göre bir avantajdır. Bir verinin %99 ihtimalle bir sınıfa ait olması, %51 ihtimalle o sınıfa ait olmasından çok farklıdır.
Logistic regression ikili sınıflandırmanın yanında çoklu sınıflandırma da yapabilir. Buna çok terimli regression denir.